Learning Persistent Community Structures in Dynamic Networks via Topological Data Analysis

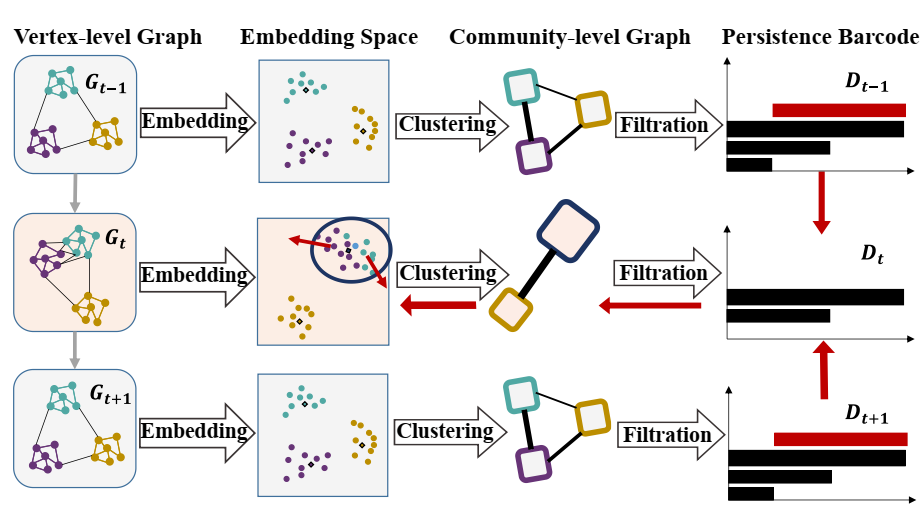
Illustration of topological regularization on an sample dynamic graph with three snapshots shown.

Abstract

Dynamic community detection methods often lack effective mechanisms to ensure temporal consistency, hindering the analysis of network evolution. In this paper, we propose a novel deep graph clustering framework with temporal consistency regularization on inter-community structures, inspired by the concept of minimal network topological changes within short intervals. Specifically, to address the representation collapse problem, we first introduce MFC, a matrix factorization-based deep graph clustering algorithm that preserves node embedding. Based on static clustering results, we construct probabilistic community networks and compute their persistence homology, a robust topological measure, to assess structural similarity between them. Moreover, a novel neural network regularization TopoReg is introduced to ensure the preservation of topological similarity between inter-community structures over time intervals. Our approach enhances temporal consistency and clustering accuracy on real-world datasets with both fixed and varying numbers of communities. It is also a pioneer application of TDA in temporally persistent community detection, offering an insightful contribution to field of network analysis.

• Project Code: GitHub link

Publication

Project list