ReadME

Programming Assigment 3

Policies

Acknowledgement: We expect you to make an honest effort to solve the problems individually. As we sometimes reuse problem set questions from previous years, covered by papers and web pages, we expect you NOT to copy, refer to, or look at the solutions in preparing your answers (relating to an unauthorized material is considered a violation of the honor principle). Similarly, we expect you not to google directly for answers (though you are free to google for knowledge about the topic). If you do happen to use other material, it must be acknowledged in your submission.
Required homework submission format: You should directly write your codes and answers in attached jupyter notebook files. Pay attention to the comments and instructions to see which parts need to be changed exactly. The teaching assistant will grade your assignment mainly based on the rightness of your programming implementation and rationality of your analytical answers.
Collaborators: If you collaborated with others on any questions, list the questions and names of collaborator. Even if you acknowledge your collaborators, your solution should be written completely using your own words.

Problem Description

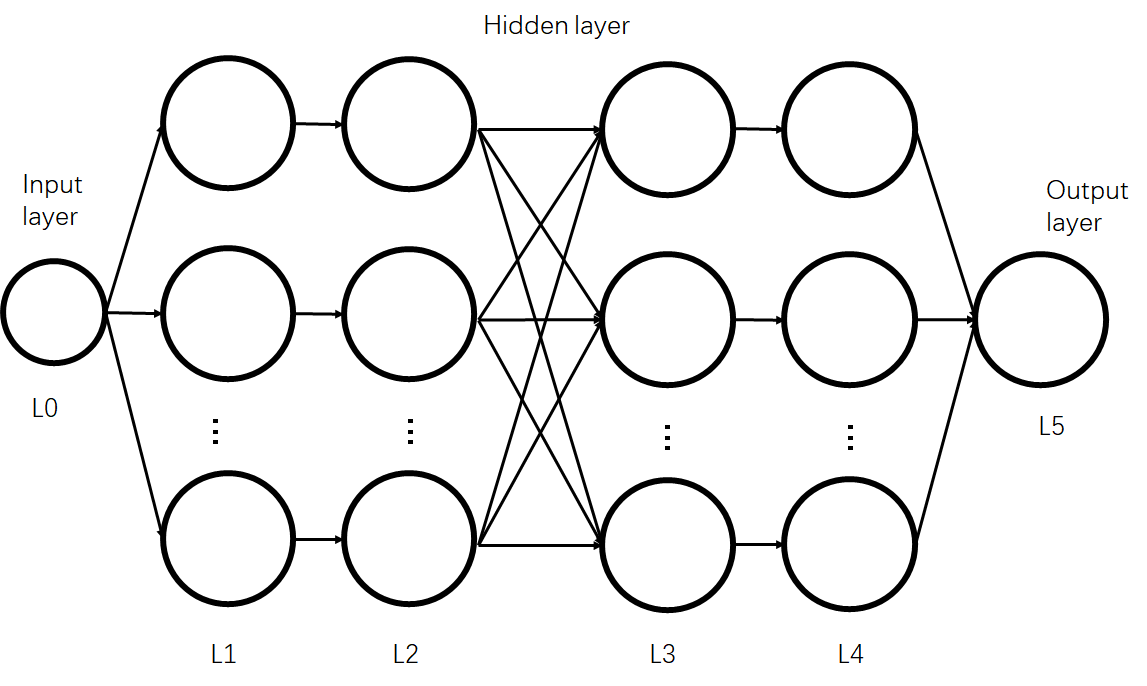
Files: download
In PA3, you need to build a simple neural network. You will see one jupyter notebook file named nn.ipynb.
You need to write your codes and answers by directly editing the file. If you have trouble to deal with jupyter notebook, ask TA (wlsdzyzl@163.com) for help. And you are expected to only use numpy packages to implement the algorithms.
After finishing your assignment, you should pack all related files into one zip file. Note that nn.ipynb must be included. Then submit it to the THU's web learning page.

Hint on L2 Regularization

(updated on Nov 19th)

Some students are confused about where to put the l2 regularization of linear layers. You probably think about adding the regularization term when defining the MSELoss, however we cannot get the weights of linear layers in loss layer.

Actually, L2 regularization can be put in the backward propagation of linear layer when updating the weights. With L2 regularization term, our final loss function becomes:

\mathcal{L}(X, W) = \text{MSE} + \lambda\sum_{i=1}^{|L|}\|W_i\|^2_2,

Here $W_i$ is the weight of i-th layers. So the gradient of each layer's weight becomes:

\frac{\partial \mathcal L}{\partial W_i} = \frac{\partial \text{MSE}}{\partial W_i} + \lambda\frac{\partial \|W_i\|^2_2 }{\partial W_i}

The first term is computed through backward propagation, which is what we have done in linear layer. For the second term: $\frac{\partial \|W_i\|^2_2 }{\partial W_i} = W_i$ . It's only related to the weight of i-th layer. There is no need to do backward propagation for regularization. So it can be put in backward function when updating the weights.